KANNet: CVPR-2020 ¶
最新的研究来自MIT、加州理工和东北大学等顶尖机构的团队,他们于于2024年6⽉16⽇联合推出了一种创新的神经网络架构——Kolmogorov–Arnold Networks(KAN)。该团队对MLP(多层感知器)进行了一次颠覆性的改良,即将可学习的激活函数从节点(神经元)转移到了连接它们的边(权重)上,开辟了一条全新的研究道路! 在此之后7⽉、8⽉相继发表KAN-GCN、KAN-Transformer模型。

⽂档说明:https://kindxiaoming.github.io/pykan/ Github:https://github.com/KindXiaoming/pykan
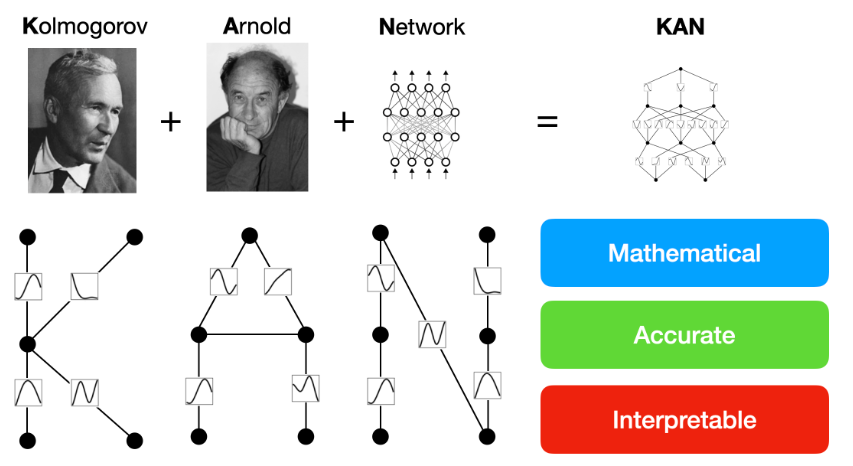
什么是 Kolmogorov-Arnold 定理?¶
Kolmogorov-Arnold 定理, ⽂叫做科尔莫⼽洛夫-阿诺尔德表⽰定理。这个定理是由苏联数学家安德烈·科尔莫⼽洛夫(Andrey Kolmogorov)⾸先提出,并由他的学⽣弗拉基⽶尔·阿诺尔德
(VladimirArnold)在1957年进⼀步发展。定理最初的动机是探讨多元函数可以如何被⼀组更简单的函数表⽰,
这是数学和理论计算机科学中的⼀个基本问题,⽽且实际上部分解答了数学家希尔伯特著名的23个问题中的第13个问题:是否可以使⽤加,减,乘,除,以及最多两个变量的代数函数的组合来求解7次⽅程。
具体来说, Kolmogorov-Arnold 定理指的是,对于任何定义在闭区间 上的连续函数:
$$
f(x_1, x_2, \dots, x_N) = \exp\left( \frac{1}{N} \sum_{i=1}^{N} \sin^2(x_i) \right)
$$
存在整数以及⼀系列的⼀维连续函数和 ,使得该多变量函数可以表⽰为:
$$
f(X) = f(x_1, \dots, x_n) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^{n} \varphi_{q,p}(x_p) \right)
$$
以上公式,举个栗⼦
假设我们有个多元函数:
$$
f(x, y, z) = x^2 + 2y^3 + \sin(z)
$$
根据kan定理,我们可以找到⼀组⼀维函数 ,使得$f(x, y, z)$可以被表⽰为以下函数的组合:
$$
f(x, y, z) = \sum_{q=1}^{7} \Phi_q \left( \sum_{p=1}^{3} \varphi_{q,p}(x_p) \right)
$$
此时,x1 = x/x2 = y/x3 = z 可以表⽰为以下具体的函数形式:
$$
\Phi_{1,1}(x) = x^2, \quad \Phi_{1,2}(y) = 0, \quad \Phi_{1,3}(z) = 0
$$
$$
\Phi_{2,1}(x) = 0, \quad \Phi_{2,2}(y) = y^3, \quad \Phi_{2,3}(z) = 0
$$
$$
\Phi_{3,1}(x) = x^2, \quad \Phi_{3,2}(y) = 0, \quad \Phi_{3,3}(z) = \sin(z)
$$
相应地, 函数可以选择为:
$$
\Phi_1(u) = u, \quad \Phi_2(u) = 2u, \quad \Phi_3(u) = u
$$
所以,f(x,y,z)可以表⽰为:
$$
f(x, y, z) = 2x_1^2 + 2y^3 + \sin(z)
$$
该定理能干什么?¶
该定理表明了真正的多元函数是⼀种求和,所有多元函数都可以表⽰为单变量函数求和的形式。这
种结构简化了多维函数的复杂性,因为⼀维函数相对来说更易于处理和学习。从机器学习和神经⽹络
的⻆度看,这提供了⼀种潜在的⽹络架构设计思路,即通过学习⼀系列的⼀维函数来近似复杂的多维函数,所以有了KAN模型。
MLP多层感知机¶
MLP ⽹络模型,也就是多层感知机。它是深度神经⽹络(DNN)的⼀种形式。MLP由多个层组成,
每⼀层都包含多个神经元,这些神经元通过激活函数进⾏⾮线性变换。MLP包括三种主要的层:
1. 输⼊层:负责接收样本数据。每个神经元代表输⼊数据的⼀个特征。
2. 隐藏层:⼀个或多个隐藏层,每层包含多个神经元。隐藏层是MLP的核⼼,它们能够学习输⼊数据
中的⾮线性特征和模式。每个隐藏层的输出都作为下⼀层的输⼊。
3. 输出层:将神经⽹络的输出呈现给外界。输出层的设计取决于特定任务⸺例如,分类任务通常⽤
具有softmax激活函数的输出层,⽽回归任务则可能使⽤⼀个没有激活函数或使⽤线性激活函数的单个节点。
在 Transformer 架构中,有着⾃注意⼒层和前馈层,其中每个⾃注意⼒层后⾯通常就会跟着⼀个
MLP 块, 这个 MLP 块也被称作前馈⽹络(Feed Forward Network, FFN)。比如EfficientVit
模型就是通过在每个⼩的块中通过减少多头注意⼒并增加FFN到3个来减少内存访问,从⽽增加模型的
推理速度。MLP 的存在为模型提供了处理复杂任务所需的计算和表达能⼒。通过这种结构,
Transformer 能够有效地处理各种序列化数据,并在多个领域,如⾃然语⾔处理、图像识别和时间序
列分析中,展⽰出极佳的表现。
MLP 是基于通⽤近似定理(Universal Approximation Theorem) ,也可翻译叫做万能近似定
理,这个定理是George Cybenko(乔治) 于1989年对使⽤sigmoid激活函数的神经⽹络证明了这⼀
定理。紧接着,Kurt Hornik(库尔特-霍尼克)在1991年扩展了这⼀结果,证明了使⽤任意⾮线性激
活函数的神经⽹络也具有通⽤近似能⼒。
定理的主要内容是:
“对于任何在闭区间上定义的连续函数和任意的误差 ,都存在⼀个具有⾄少⼀个隐藏层的前馈神经
⽹络,可以找到⼀组权重和偏置,使得该神经⽹络的输出函数在整个定义域内与⽬标函数的最⼤偏差
⼩于1 。”
这个定理解释了为什么神经⽹络可以被应⽤于各种复杂的模式识别和⾮线性回归任务,但在实际应
⽤中,如何设计⽹络结构、选择合适的激活函数和训练算法以达到所需的逼近精度仍然是重要的研究
和⼯程问题。此外,定理并没有涉及⽹络训练的收敛速度或是所需的训练数据量,因此它也有着它的局限性。
因为有着不⾜,所以我们可以改善它,或者做⼀个完全不同的东西取代他。
KAN结构推理¶
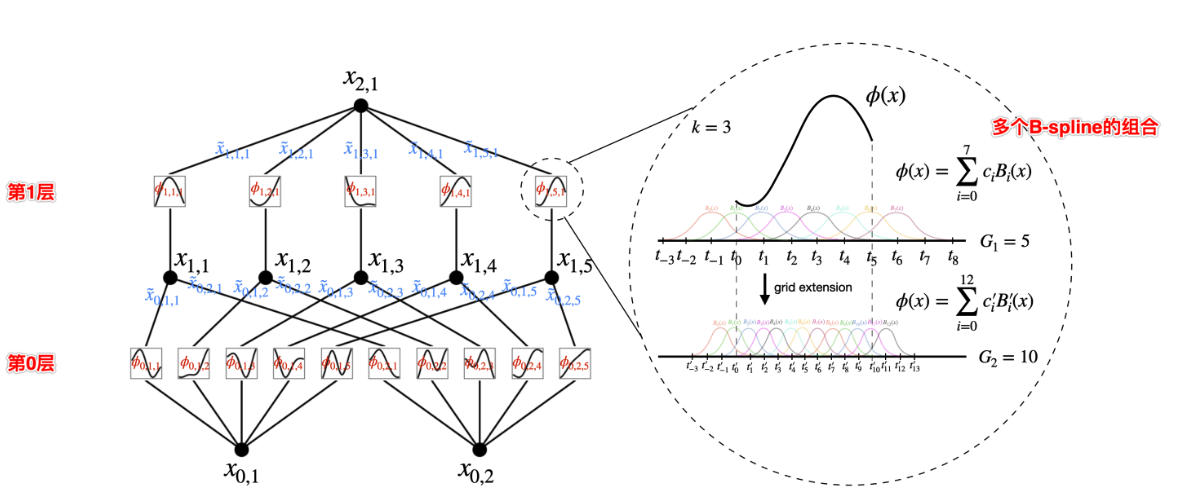
论⽂中作者给出了⼀个两层的KAN模型,左侧展⽰了⽹络的层次结构和数据流动,右边则详细描述了⼀个关键的组件⸺B-样条激活函数
(核⼼),并展⽰了如何通过“⽹格扩展技术”在粗糙和细致⽹格之间切换。
左侧的图显⽰了 KAN 的分层架构。每层包括⼀组节点,每个节点都通过⼀组特定的函数处理输⼊数
据,输出到下⼀层。每个节点上的⼩图标表⽰的是激活函数的形式,这⾥⽤B-样条函数作为激活函
数。右侧的图展⽰了⼀个激活函数 ϕ(x),它被参数化为⼀个B-样条函数。图中还展⽰了如何通过改变
B-样条的节点(也称为控制点)数量来调整函数的粒度。
这张图的核⼼在于展⽰KAN如何通过使⽤B-样条作为激活函数,结合⽹络的多层结构和激活函数的
动态调整(⽹格扩展技术),来处理复杂的⾼维数据。这种设计使得⽹络不仅能适应不同的数据分辨
率,还能通过调整激活函数的精度来优化性能。
补充:
B-样条是样条曲线⼀种特殊的表⽰形式。它是B-样条基曲线的线性组合。B-样条是⻉兹曲线的⼀种
⼀般化,可以进⼀步推⼴为⾮均匀有理B样条(NURBS),使得我们能给更多⼀般的⼏何体建造精确的模型。
KAN模型细节推导:
按照论⽂解释,KAN 层被定义为包含多个⼀维函数的矩阵,这些函数之间可以训练和调整。每个函
数不仅处理单⼀的输⼊输出关系,⽽是可以处理多个输⼊到多个输出的映射。这与 MLP 中每层处理多
个输⼊和输出的⽅式相似,但 KAN 中使⽤的是⼀维函数的矩阵:
$$
\Phi = \{ \varphi_{q,p} \}, \quad p = 1, 2, \dots, n_{\text{in}}, \quad q = 1, 2, \dots, n_{\text{out}}
$$
其中 p 是输⼊维度的索引,q 是输出维度的索引。这种矩阵形式允许KAN⽹络在每个层上实现复杂
的多维输⼊到多维输出的映射。对于 KAN 的参数和层结构,每个函数都有可训练的参数,使得 KAN 可
以通过学习优化这些函数以适应具体的数据模式。构建更深层的 KAN 就像在
MLP 中添加更多层⼀样简单。每⼀层的输出可以作为下⼀层的输⼊,通过这种⽅式,KAN能够实现更
复杂的数据表⽰和处理。论⽂指出,通过叠加更多的KAN层,可以实现对更复杂函数的⾼精度逼近。
假设:
⼀个$L+1$层的KAN复合⽹络,每⼀层的节点数是$[n_0, n_1, · · · , n_L]$;使⽤$(L, j)$表⽰第l层中的第$j$个神
经元,使⽤$x(L, j)$表⽰这个神经元的值。
KAN某层与下⼀层的联系:
KAN的第L层和第L+1层,两层之间的神经元相互连接,共存在(nL* nL+1)个激活函数,因为在KAN
中每⼀个权重都是可学习的激活函数。所以,第 L 层中第 j 个神经元(L, j) 与 第 L+1 层中第 i个神经元(L
+ 1, i),通过激活函数连接,激活函数表⽰为:Φ(L, i, j).
如果进⼀步计算x(L+1, j) ,可通过以下式⼦:第L+1层的每⼀个神经元的值都由第L层的值构成
(全连接),因KAN将激活函数放置在边上,所以来⾃第L层的值都会对应⼀个激活函数$Φ(L, i, j)$,
$i = [0,1,2,...,n_L]$,每个值经过对应的激活函数处理后,简单求和就得到了x(L+1, j).
MLP VS KAN¶
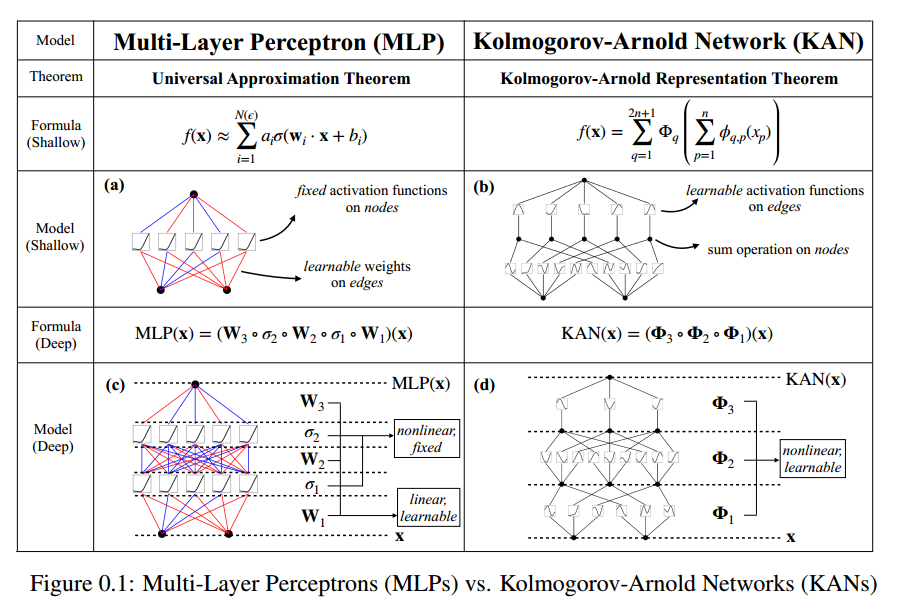
上⾯这张图就是论⽂中对于 MLPs和 KANs的对⽐。两者区别在于:MLPs 在节点,也就是神经元
上放置固定的激活函数,⽽ KANs 在边缘(权重)上放置的是可学习的激活函数。因此,KAN⽹络完
全没有线性权重矩阵:每个权重参数都由⼀种可学习的⼀维样条函数替代。KAN⽹络的节点仅对输⼊
信号进⾏求和,不进⾏任何⾮线性处理。⽽且 KANs通常允许⽐ MLPs 更⼩的计算图,⽂中也⽤ PDE
求解作为⽰例进⾏了说明:1个2层宽度为10的 KAN ⽐ ⼀个4层宽度为100的 MLP 精度⾼100倍且参数效率⾼100倍。
这里,我们可以知道这篇论⽂的贡献不只是使⽤ Kolmogorov-Arnold 表⽰定理来构建神经⽹
络,⽽是将原始的 Kolmogorov-Arnold 推⼴到任意宽度和深度。KANs 的实质可以理解成样条和
MLPs 的组合,那么结合后可以得到他们各⾃的优势。
KAN与EEG SOTA结合并处理EEG¶
问题⼀:KAN模型能否处理EEG数据,⽤于分类或预测任务?
1. ⾼维数据处理:KAN模型在处理⾼维数据时能够打破“维度的诅咒”,这在处理EEG数据
时可能是有益的,因为EEG数据通常是⾼维的。
2. 可解释性:由于KAN模型的可解释性,它可以提供关于脑电数据分类或预测任务的洞察,
帮助研究⼈员理解模型的决策过程。
3. 准确性:如果EEG数据的分类或预测任务可以从KAN模型的架构中受益,那么KAN模型可
能会提供⽐传统MLP更准确的结果。
4. 学习复杂函数:由于KAN模型能够学习复杂的单变量函数,它可能适合捕捉EEG数据中的
复杂模式。
5. ⼩规模⽹络表现:论⽂中提到,⼩型KAN模型在某些任务中可以与⼤型MLP模型相媲美或
更好,这可能意味着在处理EEG数据时可以使⽤更加轻量级的⽹络,从⽽减少计算资源的
需求。
问题⼆:KAN模型的可解释性如何帮助我们理解EEG数据的分类或预测?
2.1 直观的可视化:KAN模型的架构允许直观地可视化⽹络中的激活函数。通过观察这些激活
函数,我们可以直接看到模型在处理EEG数据时哪些特征被激活,以及它们是如何组合的。
这种可视化有助于理解模型是如何识别和处理脑电信号中的模式。
2.2 边缘上的可学习激活函数:在KAN模型中,激活函数是放置在⽹络边缘上的,这意味着每
个连接都有⼀个可学习的函数,⽽不是⼀个固定的⾮线性激活。这种设计提供了更细粒度的
控制,允许模型捕捉到EEG数据中更复杂的动态变化。
2.3 交互式探索:KAN模型⽀持与⽤⼾交互,允许使⽤者⼿动调整和优化⽹络中的激活函数。
例如,我们可以基于先验知识或直觉修改某些激活函数,然后让模型去测试这些假设。这种
交互性有助于研究⼈员将领域知识融⼊模型中,提⾼对EEG数据分类或预测的理解。
2.4 简化和符号化:KAN模型提供了⼯具来简化⽹络结构,并将学到的激活函数转换为符号形
式。这可以帮助我们发现EEG数据中的潜在数学、科学关系,例如,某些脑电波形可能与特
定的认知状态或疾病状态相关联。
2.5 稀疏性和选择性:通过使⽤正则化技术,KAN模型可以被训练为只有少数激活函数在起作
⽤,这有助于识别EEG数据中最关键的特征。这种稀疏性不仅提⾼了模型的可解释性,还可
能提⾼其泛化能⼒。
2.6 局部性:由于KAN模型使⽤的是局部基函数(如样条),每个样本只影响少数附近的系
数,这有助于保护已学习的知识不被新数据覆盖。在EEG数据分析中,这意味着模型可以逐
步学习不同的脑电模式,⽽不会忘记之前学到的信息。
KAN与EEGNet结合点:
1. 混合架构:可以设计⼀个混合模型,其中EEGNet负责提取EEG信号的初步特征,⽽KAN模型则⽤于
进⼀步处理这些特征,以提⾼分类或预测的性能。EEGNet的卷积层可以捕捉到EEG信号中的空间和
时间特征,⽽KAN模型的可学习激活函数可以捕捉到更复杂的⾮线性关系。
2. 特征融合:在EEGNet和KAN之间引⼊⼀个特征融合层,将EEGNet提取的特征与KAN模型学习到的
激活函数进⾏结合。这种融合可以增强模型对EEG信号中复杂模式的识别能⼒。
3. 可解释性增强说明:EEGNet等深度学习模型通常被认为是“⿊箱”,⽽KAN模型的可解释性可以
⽤来解释EEGNet的决策过程。通过将KAN模型的可视化和解释能⼒与EEGNet的预测能⼒相结合,
可以提⾼模型的透明度和可信度。
4. 优化激活函数:EEGNet中的激活函数通常是固定的,如ReLU或Sigmoid。通过将这些激活函数替
换为KAN模型中的可学习激活函数,可以使模型更好地适应EEG数据的复杂性,从⽽可能提⾼分类性能。
5. 局部性利⽤:KAN模型的局部性特性可以⽤来增强EEGNet模型的局部特征学习能⼒。例如,可以
在EEGNet的卷积层中引⼊局部连接,模仿KAN模型中的样条激活函数,以提⾼对局部脑电活动的敏感性。
6. 跨任务学习:如果EEG数据被⽤于多个不同的任务(例如,不同的疾病分类或不同的⽣理状态监
测),KAN模型的可解释性和灵活性可以⽤来在这些任务之间迁移知识,提⾼模型在新任务上的泛化能⼒。